Miếng đất sét 3.700 năm tuổi đã giúp chứng minh định lý Pitago đã được ứng dụng trước khi nhà triết học Pythagoras ra đời
Ngay cả khi Pythagoras chưa ra đời, người dân vùng đất văn minh Lưỡng Hà đã biết ứng dụng Định lý Pitago.

Ngay cả khi bạn không phải là một nhà toán học, bạn có thể đã được thầy cô dạy về định lý Pitago trong trường học. Đây là phương pháp tính độ dài các cạnh tam giác vuông được đặt tên của nhà toán học và triết học người Hy Lạp - Pythagoras vào thế kỷ thứ 6 trước Công nguyên. Hóa ra kiến thức này đã từng được áp dụng trước cả thời của Pythagoras.
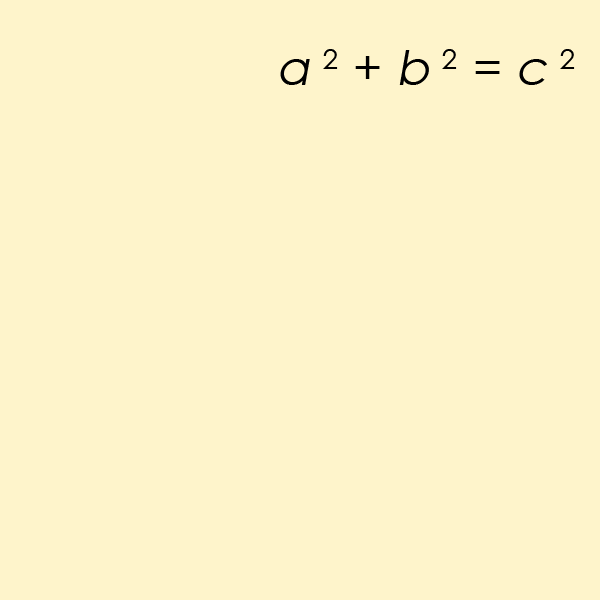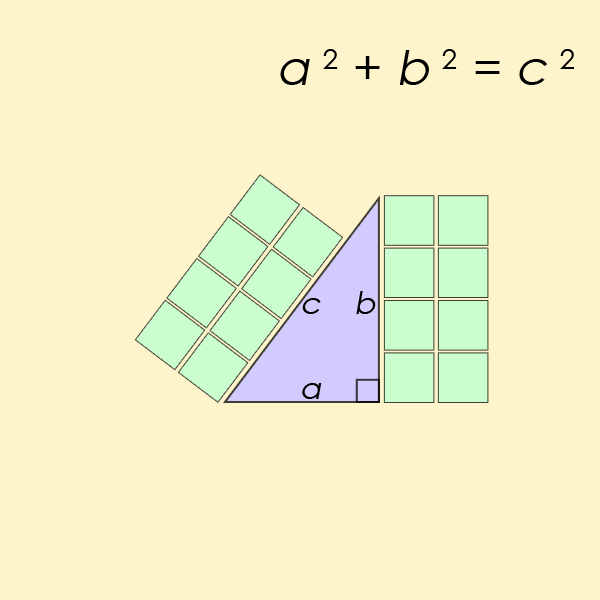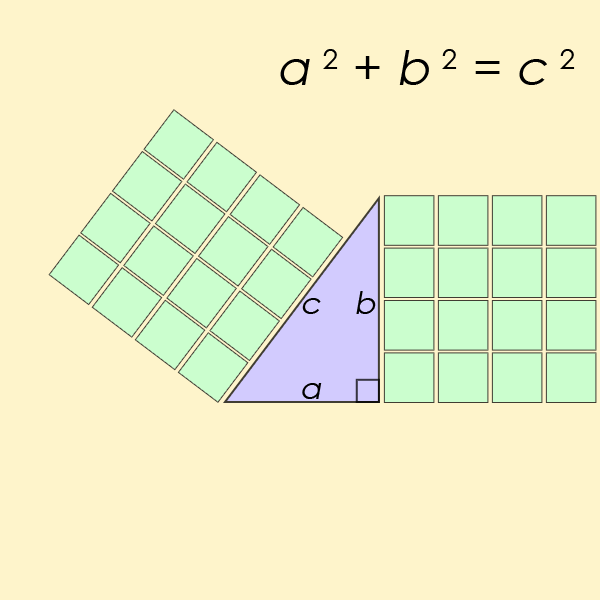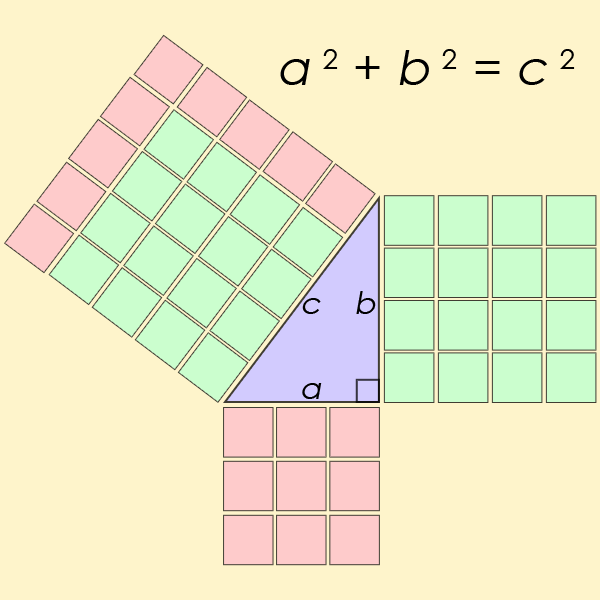
Minh họa Định lý Pitago
Một bài báo gần đây được xuất bản trên tạp chí Science Foundation đã đăng tải hình ảnh một "máy tính bảng" làm bằng đất sét từ thời Babylon cổ đại, nhờ đó mà các nhà khảo sát phát hiện ra rằng, người Lưỡng Hà đã sử dụng công thức tương tự như định lý Pitago để phân chia chính xác vùng đất của họ tạm gọi là bộ ba số Pitago (Pythagorean triples). Vào năm 2018, Tiến sĩ Daniel Mansfield thuộc Trường Toán học và Thống kê tại Đại học New South Wales phát hiện ra hiện vật này trong bộ sưu tập của Bảo tàng Khảo cổ học Istanbul ở Thổ Nhĩ Kỳ.

Miếng đất sét thời Babylon cổ đại có niên đại 3.700 năm tuổi đã tiết lộ rằng, người Babylon cổ đại đã hiểu và sử dụng định lý Pitago hơn 1.000 năm trước khi nhà triết học Pythagoras ra đời
Bộ ba số Pitago là một tập hợp các số thỏa mãn công thức tính độ dài các cạnh của một tam giác vuông. Ví dụ đơn giản nhất là tập hợp các số 3, 4 và 5. Số lớn nhất trong bộ ba Pitago luôn là cạnh huyền, hoặc cạnh đối diện với góc vuông 90 độ. 3 bình phương là 9; 4 bình phương là 16. Cộng lại với nhau, tạo thành 25, là bình phương của cạnh huyền (5). Hình tam giác có chân là 3 và 4 và cạnh huyền có chiều dài là 5 sẽ luôn có một góc vuông hoàn hảo.
Được biết đến với cái tên Si.427, miếng đất sét chứa một sơ đồ và văn tự hình nêm (một hệ thống chữ viết cổ). Người tạo ra nó được cho là một nhà khảo sát đất đai trong thời kỳ Babylon cổ từ năm 1900 đến 1600 trước Công nguyên nhờ dấu hiệu được khắc bằng những đường nét của chữ viết. Theo Tiến sĩ Mansfield, "Đó là ví dụ duy nhất được biết đến về tài liệu địa chính từ thời kỳ Babylon cổ đại, là một cách được các nhà khảo sát sử dụng để xác định ranh giới đất đai".

Những người khảo sát địa chất đã ứng dụng bộ ba số Pitago để vẽ những góc vuông hoàn hảo
Tuy nhiên, đây không phải là lý do duy nhất mà miếng đất sét này trở thành một hiện vật lịch sử đặc biệt. Tiến sĩ Mansfield nhận thấy rằng các hình tam giác và hình chữ nhật được khắc lên đất sét các góc vuông rất hoàn hảo. Điều này cho thấy người khảo sát đã có một phương pháp toán học rất chặt chẽ. Sau khi kiểm tra kỹ hơn, tiến sĩ Mansfield nhận ra người khảo sát đã sử dụng bộ ba số Pitago để tạo ra các tam giác vuông. Chúng có thể được thu nhỏ thành bất kỳ kích thước nào miễn là tỷ lệ các cạnh được duy trì. Hai hình tam giác có cùng kích thước cũng có thể tạo thành một trường hình chữ nhật.

Mặc dù "máy tính bảng" không thể hiện định lý Pitago ở dạng đại số quen thuộc như biểu thị thời nay, nhưng việc tạo ra các bộ ba này đòi hỏi phải hiểu nguyên tắc chung chi phối mối quan hệ giữa độ dài các cạnh tam giác vuông và cạnh huyền
Khám phá này là bằng chứng về việc sử dụng hình học ứng dụng đầu tiên được biết đến, hơn một nghìn năm trước thời Pythagoras được sinh ra. Trong khi người Hy Lạp phát triển lượng giác (nghiên cứu về hình tam giác) cho lĩnh vực thiên văn học, thì bằng việc ứng dụng hình tam giác của người Babylon cổ đại này dường như là thực tiễn hơn rất nhiều. Khi đất đai được tư nhân hóa, các tranh chấp về ranh giới đòi hỏi các phương pháp phân định và giải quyết phức tạp và công bằng. Tuy nhiên, hệ thống số của Babylon bị hạn chế bởi vì họ chỉ có thể sử dụng tối đa 60 số, có nghĩa là những người khảo sát bị giới hạn trong bộ ba số Pitago.

Người ta thường cho rằng, lượng giác, một nhánh toán học liên quan đến việc nghiên cứu các hình tam giác, được phát triển bởi những người Hy Lạp cổ đại. Tuy nhiên, người Babylon đã phát triển phương pháp "lượng giác proto" thay thế theo cách của riêng họ để giải quyết các vấn đề liên quan đến đo đạc đất đai"
Số của người Babylon cổ được viết bằng cách tích lũy các ký hiệu đại diện cho 10 và 1 theo thứ tự. Ví dụ, 16 được viết là một 10 sau đó là 6 số 1. Tương tự, 5 được viết là không có số 10, theo sau là 5 số 1, còn ngày nay chúng ta viết các số này bằng: 00,01,02,03,..., 58 và 59.
Một miếng đất sét khác có tên là Plimpton 322 đã viết ra một danh sách các bộ ba trong cùng một bảng. Tiến sĩ Mansfield đã tìm thấy miếng này vào năm 2017 qua bộ sưu tập của Đại học Columbia. Mặc dù ông cho rằng nó có khả năng được sử dụng để hướng dẫn các dự án xây dựng, nhưng đây cũng là minh chứng cho nỗ lực của người xưa nhằm tạo ra tất cả các bộ ba số Pitago. Tiến sĩ Mansfield nói, "Sự hiểu biết sâu sắc và mang tính số học cao về ứng dụng thực tế của hình chữ nhật được đặt tên là 'lượng giác proto' nhưng nó hoàn toàn khác với lượng giác hiện đại của chúng ta liên quan đến sin, cos và tan."

Điều gì tiếp theo sau một khám phá hấp dẫn như vậy? Lịch sử ban đầu của toán học đòi hỏi một số sửa đổi nghiêm túc. Việc sử dụng rõ ràng các bộ ba số Pitago trong thời kỳ Babylon cổ là một sự điều chỉnh lớn đối với các mốc thời gian đã được thiết lập của hình học. Điều này đặt ra câu hỏi, đối với Tiến sĩ Mansfield và những người khác, về những khám phá toán học lớn nào khác có thể nằm trong bộ sưu tập của các bảo tàng trên khắp thế giới.
Các chuyên gia từ lâu đã biết rằng, người Hy Lạp kế thừa giáo lý toán học từ người Ai Cập, trong khi người Ai Cập đón nhận chúng từ người Babylon. Tuy nhiên, điều đáng ngạc nhiên đối với ông Mansfield là mức độ tinh vi về mặt lý thuyết của những "máy tính bảng" mà người Babylon cổ đại đã phát minh và sử dụng ở giai đoạn đầu của lịch sử loài người.


