99% người thông minh nhất cũng "nhũn não" với 8 câu đố này của ảo thuật gia Martin Gardner

Martin Gardner (1914 – 2010) là ảo thuật gia người Mỹ. Ông được đánh giá là một trong những người có đóng góp quan trọng nhất cho nền ảo thuật thế kỷ 20. Bên cạnh niềm đam mê dành cho ảo thuật, Martin Gardner còn đặc biệt nổi tiếng qua những bài toán đố, thử thách trí thông minh và tài suy luận.

Những bài toán của ông khơi gợi niềm đam mê toán học cho nhiều người bằng niềm vui khám phá từ câu đố tưởng dễ mà lại không dễ chút nào.

Mời bạn đọc cùng thử sức với 8 bài toán nổi tiếng nhất của Martin Gardner:

1. Đường cắt “xoắn não”

Bạn hãy cắt hoặc vẽ một đường, không cần thẳng, để chia hình màu xanh thành hai phần giống hệt nhau.

Đáp án:

2. Những đôi tất màu sắc

Trong ngăn kéo có 10 đôi tất màu đỏ và 10 đôi tất màu xanh. 20 chiếc tất giống hệt nhau, trừ màu sắc của chúng. Trong căn phòng tối không một chút ánh sáng, bạn cần lấy được 2 chiếc tất đồng màu. Bạn phải lấy ít nhất bao nhiêu chiếc tất ra khỏi ngăn kéo để thành công?

Ảnh minh họa.

Đáp án: 3 chiếc tất

Giải thích: Với 2 chiếc tất, bạn có cơ hội có 1 đỏ + 1 xanh hoặc 1 cặp đồng màu. Với 3 chiếc tất, chắc chắn bạn sẽ có 1 cặp đồng màu và 1 chiếc khác màu.

3. Bu-lông xoắn ốc

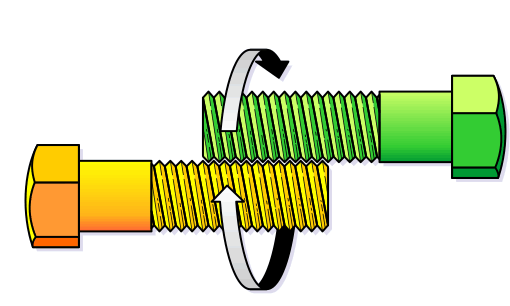
Có 2 bu-lông giống hệt nhau được xếp sao cho các rãnh xoắn ốc của nó khớp nhau như trong hình. Cầm chắc đầu 2 bu-lông, di chuyển chúng theo hướng mũi tên (lưu ý không được để phần đầu các bu-lông xoay vòng), như vậy thì các đầu bu-lông sẽ:

Chọn đáp án đúng:

(1) Di chuyển hướng vào trong

(2) Di chuyển hướng ra ngoài

(3) Giữ nguyên khoảng cách giữa chúng

Đáp án: (3) Đầu bu-lông sẽ không di chuyển hướng ra ngoài hay vào trong.

Giải thích: Chuyển động của 2 bu-lông sẽ triệt tiêu lẫn nhau – giống như khi một người bước lên thang cuốn theo hướng đi lên với cùng vận tốc hướng đi xuống của nó thì vị trí của bạn so với 2 đầu thang cuốn sẽ giữ nguyên. Nếu bạn có sẵn 2 bu-lông, ốc vít, hãy thử xem nhé!

4. Ngã ba đường

Một nhà logic học đi du lịch ở vùng biển phía Nam. Ông bị lạc trên hòn đảo là nơi sinh sống của hai bộ tộc Dối trá và Thành thật. Thành viên trong bộ tộc Dối trá luôn nói dối còn người của Thành thật luôn nói thật. Nhà logic học muốn đi đến một ngôi làng nhưng khi đứng trước ngã ba, ông không biết đường và phải hỏi người dân địa phương. Tuy nhiên, ông không biết anh ta thuộc bộ tộc nào. Suy nghĩ một lát, ông hỏi một câu duy nhất. Sau khi nhận được câu trả lời, ông tìm đúng hướng đi.

Vậy, nhà logic học đã hỏi anh ta câu gì?

Đáp án: Ông chỉ vào một trong hai hướng và hỏi: “Nếu tôi hỏi anh, con đường này có dẫn tới làng không, anh sẽ trả lời là “đúng” chứ?”.

Giải thích: Mấu chốt ở đây đó là phải tìm ra câu hỏi khiến người nói dối phải nói dối về một lời nói dối từ đó có được đáp án đúng.

Nếu con đường mà nhà logic chỉ là đúng, người thuộc bộ tộc nói dối sẽ trả lời là “không” cho câu hỏi “con đường này có dẫn tới làng không?” nhưng là một người chuyên nói dối, anh ta sẽ trả lời “đúng” cho câu hỏi “cậu sẽ trả lời “đúng” chứ?”.

Nếu con đường mà nhà logic chỉ là sai, người thuộc bộ tộc nói dối sẽ trả lời “đúng” cho câu hỏi “con đường này có dẫn tới làng không” nhưng là một người chuyên nói dối, anh ta sẽ trả lời “không đúng” cho câu hỏi “cậu sẽ trả lời “đúng” chứ?”.

Nếu gặp người thuộc bộ tộc nói thật thì họ sẽ luôn nói thật và nhà logic sẽ dễ dàng chọn được con đường đúng để đi.

5. Ba hình vuông

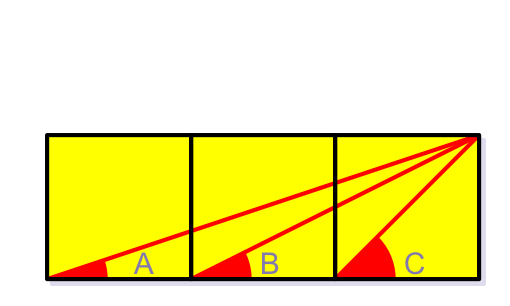
Sử dụng kiến thức hình học cấp 1 (không dùng lượng giác) để chứng minh góc C bằng tổng góc A và góc B

Đáp án: Đây là một cách để chứng minh:

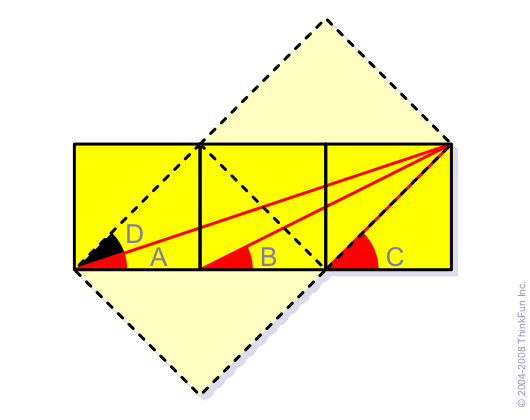
Vẽ thêm các hình vuông (đường gạch nối), góc C sẽ bằng tổng góc A + góc D do cả 2 góc đều được tạo nên bằng cách cắt hình vuông bằng 1 đường chéo. Góc B bằng góc D bởi chúng đều là góc của tam giác được tạo bằng cách cắt đôi hình chữ nhật do 2 hình vuông ghép lại tạo thành. Như vậy góc B có thể thay được góc D, suy ra: A + D = A + B = C (điều phải chứng minh).

6. Bài toán cắt bánh

Với một nhát cắt, bạn có thể chia một chiếc bánh thành hai phần. Cắt thêm một nhát nữa, bánh được chia làm 4 phần. Đến nhát cắt thứ ba, bạn có nhiều nhất là 7 phần. Vậy với 6 lần cắt, bạn có thể chia chiếc bánh thành tối đa bao nhiêu phần?

Đáp án: 22 phần

Giải thích: Bạn có thể giải bài toán bằng phương pháp thực hành, nghĩa là cắt một cái bánh rồi đếm số phần hoặc vẽ hình một chiếc bánh và thử. Tuy nhiên, phương pháp này có thể đưa ra đáp án sai nếu cách cắt của bạn không đúng.

Vì thế, bạn nên sử dụng phương pháp suy luận để tìm ra mối liên quan giữa số lần cắt và số phần bánh tăng thêm.

Với một nhát cắt, bánh được chia làm hai phần.

Thêm nhát thứ hai, số phần tăng thêm hai thành 4 phần.

Lần cắt thứ ba, số phần tối đa 7 phần, tăng thêm 3 phần.

Có thể thấy, số phần bánh tăng thêm bằng số nhát cắt. Vì vậy, nhát thứ tư tạo thêm 4 phần. Lần cắt thứ năm, số phần bánh tăng thêm 5. Ở lần cắt thứ sáu, số lượng phần bánh tối đa là: 1 + 1 + 2+ 3 + 4 + 5 + 6 = 22.

7. Bàn cờ bị cắt xén

Bạn có một bàn cờ và 32 quân cờ domino. Kích thước của mỗi quân cờ domino bằng diện tích của 2 ô vuông trên bàn cờ. Như vậy, 32 quân cờ có thể phủ kín 64 ô vuông trên bàn cờ.

Người ta cắt 2 ô ở 2 góc đối diện của bàn cờ và bỏ bớt 1 quân cờ. Ta có thể dùng 31 quân cờ che kín 62 ô cờ hay không và bằng cách nào? Nếu không thì về sao?

Đáp án: Bàn cờ thiếu đi hai góc đối diện (còn 62 ô) thì sẽ không thể che kín bằng 31 quân cờ domino

Giải thích: Có thể thấy rằng, mỗi quân domino luôn nằm trên hai ô liền kề có màu sắc khác nhau. Trong khi đó, hai ô bị cắt có màu sắc giống nhau. Vì thế, sau khi che kín 60 ô, hai ô còn lại sẽ cùng màu.

Hơn nữa, do màu sắc của hai ô liền kề khác nhau nên nếu hai ô còn lại cùng màu, chúng sẽ nằm cách xa nhau. Ta không thể dùng một quân domino để che kín hai ô này.

8. 2 hình xoắn ốc

Một hình xoắn ốc được tạo nên từ một sợi dây, hai đầu dây chạm nhau. Hình còn lại được tạo nên từ hai sợi dây riêng rẽ, hai đầu của mỗi dây cũng chạm nhau. Bạn có thể phân biệt hình nào dùng một dây, hình nào dùng hai dây bằng mắt thường mà không dùng bút vẽ hay không?

Đáp án: Hình xoắn ốc bên trái tạo nên từ một dây.

Theo Nguyễn Nguyễn