Ngày xưa đi học không phải bạn dốt toán đâu, chỉ là bạn chưa cảm nhận được vẻ đẹp của nó mà thôi

Chúng ta đều quen thuộc với bảng cửu chương, một trọng tâm giảng dạy trên toàn thế giới:

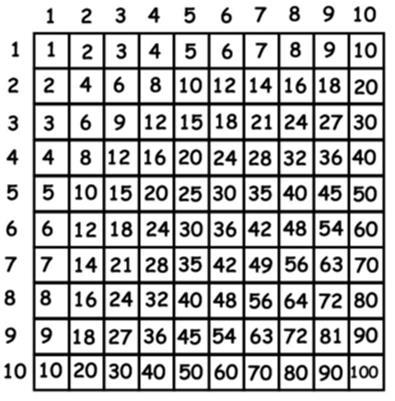
Bạn không thể phàn nàn chút gì về tính chính xác của bức ảnh này. Đó cũng là điểm ít hấp dẫn của bảng cửu chương – một tập hợp có vẻ rời rạc của những điều hiển nhiên.

Chúng được sinh ra là để mọi người tìm hiểu, ghi nhớ và nhớ lại khi cần. Tuy nhiên, đối với một nhà toán học, thì lại có vô số các mô thức và cấu trúc trong đó. Họ nhìn bức ảnh và không chỉ thấy đây là 100 con số đơn lẻ.

Có thể họ sẽ thấy hình ảnh bên dưới – một bảng cửu chương được chia tỷ lệ theo các con số:

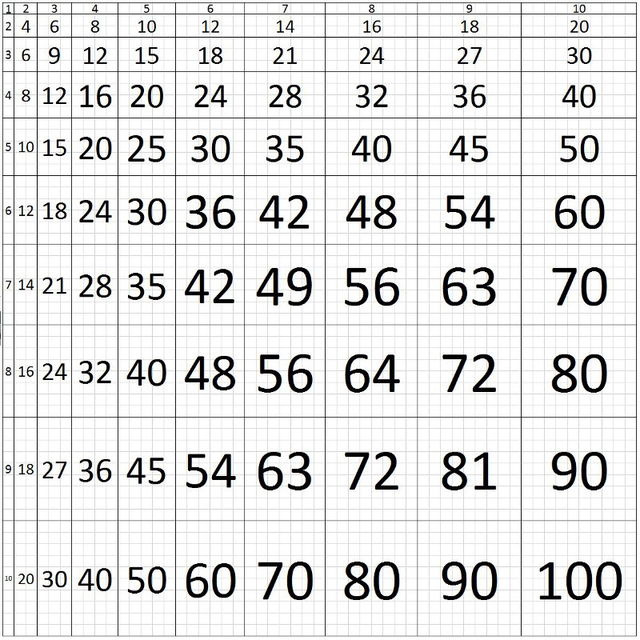
Chỉ với một thay đổi đơn giản như vậy, bảng cửu chương đã bắt đầu nói gì đó với chúng ta. Nó truyền tải kích cỡ và tỷ lệ chứ không chỉ là các con số vô tri. Nó kết nối các chủ thể rời rạc, gắn các con số với hình học; gắn phép nhân với diện tích.

Sử dụng thêm màu sắc, chúng ta có thể tạo ra một loại cấu trúc mới – một sự kết hợp của các bảng cửu chương nhỏ hơn:

Kích cỡ và hình dáng của mỗi lớp số lại bộc lộ những điều mới. Thường thì nó thể hiện điều ta đã biết nhưng theo một cách mới. Vì thế, có được hình dung đúng đắn chính là chìa khóa để mở ra những tiềm năng toán học trong bộ óc của bạn.

Trong cuốn sách “Outliers”, Malcolm Gladwell đã khẳng định để thành thạo thứ gì đó, bạn cần 10.000 giờ thực hành. Điểm cốt yếu của quá trình thực hành là nó giúp ta phát triển những hình dung phong phú: làm thức dậy những mô thức tiên nghiệm về thông tin đã tồn tại trong ký ức lâu dài của chúng ta.

Hình dung càng mạnh mẽ và dồi dào thì chúng ta càng có cơ sở để kết nối các ý tưởng, phát triển trực giác và giải quyết các vấn đề.

Adam Grant, trong cuốn sách "Originals" của mình, cũng nêu ra một đặc điểm nổi bật của các bộ óc sáng tạo thiên tài. Đó là họ có khả năng tạo ra nhiều ý tưởng khi tiếp cận một vấn đề. Trong toán học cũng vậy: Bạn càng có khả năng giải quyết được một bài toán khó nếu có càng nhiều cách nhìn nhận vấn đề khác nhau. Những ý tưởng này xuất phát từ chính hình dung trong tâm trí của bạn. Toán học sẽ là một thực thể vô hồn nếu hình dung của chúng ta không mạnh.

Theo các nhà toán học, số nguyên tố không nhận được sự quan tâm mà chúng xứng đáng được nhận. Với chúng ta, chúng chỉ đơn giản là một tập hợp các con số chỉ có 2 ước số duy nhất; chỉ là một đối tượng trong chương trình học, dùng để tính ước chung lớn nhất, bội chung nhỏ nhất; hay các giá trị ngẫu nhiên trong các bài kiểm tra. Tuy nhiên đối với các nhà toán học, chúng lại là DNA của lĩnh vực này.

Định lý cơ bản của số học (Mọi số tự nhiên lớn hơn 1 đều có thể viết thành tích của các số nguyên tố. VD: 1200 = 24 x 3 x 52) cho ta biết rằng mỗi số nguyên đều là một sản phẩm độc nhất của các số nguyên tố. Bạn càng suy ngẫm về định lý này, thì lại càng thấy được tính ưu việt của các số nguyên tố. Có lẽ vì thế mà chúng được bao phủ bởi một bức màn huyền bí, và tạo nên những vấn đề hóc búa nhất chưa có câu trả lời trong toán học.

Nhưng sự mê mải của các nhà toán học với số nguyên tố không phải là đặc quyền của riêng họ. Với các hình dung đúng đắn, số nguyên tố có thể khai sáng, hấp dẫn và làm say mê tất cả chúng ta. Chẳng hạn, dưới đây là một bảng số do Daniel Finkel tạo ra

Như chính lời khuyên của Finkel, hãy để bảng số này nói chuyện với bạn. Hãy khám phá các mô thức. Đùa nghịch với cấu trúc của nó. Chìm đắm trong các tầng sâu của phép nhân và tìm ra vai trò trung tâm mà các số nguyên tố nắm giữ trong đó.

Nếu toán học chỉ là một mớ các biểu tượng hỗn tạp đối với bạn, hãy bình tâm khi biết rằng cả một vũ trụ những điều thú vị và đặc biệt đang chờ bạn. Trong toán học đầy rẫy những hình dung mường tượng – những yếu tố nuôi dưỡng và tạo ra sự kết nối giữa các ý tưởng. Đây chính là vẻ đẹp mà các nhà toán học mê đắm và tìm kiếm bấy lâu nay.

Đinh Vân